Compressed suffix array
In computer science, a compressed suffix array[1][2] is a compressed data structure for pattern matching. Given a text T of n characters from an alphabet Σ, the compressed suffix array support searching for arbitrary patterns in T. For an input pattern P of m characters, the search time is equal to n times the higher-order entropy of the text T, plus some extra bits to store the empirical statistical model plus o(n).
The original instantiation of the compressed suffix array[1] solved a long-standing open problem by showing that fast pattern matching was possible using only a linear-space data structure, namely, one proportional to the size of the text T, which takes 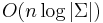 bits. The conventional suffix array and suffix tree use
bits. The conventional suffix array and suffix tree use 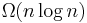 bits, which is substantially larger. The basis for the data structure is a recursive decomposition using the "neighbor function," which allows a suffix array to be represented by one of half its length. The construction is repeated multiple times until the resulting suffix array uses a linear number of bits. Following work showed that the actual storage space was related to the zeroth-order entropy and that the index supports self-indexing.[3] The space bound was further improved using adaptive coding with longer contexts to achieve the ultimate goal of higher-order entropy.[2] The space usage is extremely competitive in practice with other state-of-the-art compressors,[4] and it also supports fast pattern matching.
bits, which is substantially larger. The basis for the data structure is a recursive decomposition using the "neighbor function," which allows a suffix array to be represented by one of half its length. The construction is repeated multiple times until the resulting suffix array uses a linear number of bits. Following work showed that the actual storage space was related to the zeroth-order entropy and that the index supports self-indexing.[3] The space bound was further improved using adaptive coding with longer contexts to achieve the ultimate goal of higher-order entropy.[2] The space usage is extremely competitive in practice with other state-of-the-art compressors,[4] and it also supports fast pattern matching.
The memory accesses made by compressed suffix arrays and other compressed data structures for pattern matching are typically not localized, and thus these data structures have been notoriously hard to design efficiently for use in external memory. Recent progress using geometric duality takes advantage of the block access provided by disks to speed up the I/O time significantly[5]
References
- ^ a b R. Grossi and J. S. Vitter, Compressed Suffix Arrays and Suffix Trees, with Applications to Text Indexing and String Matching], SIAM Journal on Computing, 35(2), 2005, 378-407. An earlier version appeared in Proceedings of the 32nd ACM Symposium on Theory of Computing, May 2000, 397-406.
- ^ a b R. Grossi, A. Gupta, and J. S. Vitter, High-Order Entropy-Compressed Text Indexes, Proceedings of the 14th Annual SIAM/ACM Symposium on Discrete Algorithms, January 2003, 841-850.
- ^ K. Sadakane, Compressed Text Databases with Efficient Query Algorithms Based on the Compressed Suffix Arrays, Proceedings of the International Symposium on Algorithms and Computation, Lecture Notes in Computer Science, vol. 1969, Springer, December 2000, 410-421.
- ^ L. Foschini, R. Grossi, A. Gupta, and J. S. Vitter, Indexing Equals Compression: Experiments on Suffix Arrays and Trees, ACM Transactions on Algorithms, 2(4), 2006, 611-639.
- ^ W.-K. Hon, R. Shah, S. V. Thankachan, and J. S. Vitter, On Entropy-Compressed Text Indexing in External Memory, Proceedings of the Conference on String Processing and Information Retrieval, August 2009.